初めに
Webの世界では実世界と比べて簡単に変更を伴う実験を行うことが可能です.このため,A/Bテストを基に意思決定を行うことが一般的だと思います.A/Bテストのエビデンスレベル(科学的根拠の信頼性の程度)はシステマティックレビュー(複数のA/Bテスト結果をまとめて結論付ける)を除くと最も高く, 正しく 行ったA/Bテストの結果から,正しい意思決定を行うことが可能です.
でも実は,A/Bテストを 正しく 行うことは,様々な落とし穴が存在し結構難しくなっています.ここではやりがちでは有るのだけれども,一度覚えておけばやらかさない失敗とその対処方法について説明します.今回具体的に説明を行うのは,ランダム化の単位と分析の単位が異なる場合に,ナイーブなやり方で分散の推定を行うと分散の推定結果は過小評価されてしまう≒結果が有意になりやすくなってしまうというものです.
ランダム化の単位というのはA/Bテストにおいて,どんな粒度でそれぞれの実験(例えば,実験Aと実験B)に割り当てるのかとうことです.例えばよくあるランダム化の単位にはユーザやリクエストのようなものがあるのかなと思います.分析の単位は,どんな粒度で指標の計算を行うのかを指します.例えば,広告のクリックを例に上げると,ユーザごとにCTRを計算しその平均を取る(CTRのユーザ平均)場合と,すべてのユーザを区別せずにCTRを計算する場合があります.ランダム化の単位をユーザとし,分析の単位はすべてのユーザを区別せずCTRを計算するような場合, ランダム化の単位と分析の単位が異なり,問題が生じる可能性があります.
今回言いたかったこと
- A/Bテストのエビデンスレベルは高いものの,A/Bテストを正しく行うのは難しく,誤った結論を導いてしまう可能性がある.
- A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実験とは では,A/Bテストについて網羅的に書いてあるので,A/Bテストを頻繁に行う方は一度目を通しておくと良さそうです.
広告クリックのシミュレーションを行う
ここでは,こちらの論文を参考に,広告クリックのシミュレーションを行います.各シミュレーションにはそれぞれ1000人のユーザが存在し,ユーザは広告の表示回数やクリック率が異なる3つのグループに分けられます.
具体的なコードは以下のとおりです.
def make_exp_data(num_sim = 1000, num_user = 1000):
rng = np.random.default_rng()
sim_result = np.zeros((num_sim, num_user, 2))
for sim_i in range(num_sim):
cluster = rng.multinomial(num_user, [1./3,1./2,1./6])
for user_i in range(num_user):
# small
if user_i<cluster[0]:
lam = 2
mu = 0.3
sig = 0.05
# medium
elif user_i<cluster[0]+cluster[1]:
lam = 5
mu = 0.5
sig = 0.1
#high
else:
lam = 30
mu = 0.8
sig = 0.05
N_i = rng.poisson(lam=lam)
mu_i = rng.normal(loc=mu, scale=sig)
try:
Y_i = rng.binomial(N_i, mu_i)
except:
Y_i = N_i
sim_result[sim_i, user_i, :] = [N_i, Y_i]
return sim_result
上記のシミュレーションを実験A,実験Bそれぞれ全く同じパラメータでシミュレーションを行い,以下では両群には差が無い状況(≒A/Aテスト)を考えます.
ナイーブなやり方で検定を行う場合
ここでは,2つの実験に差がない状況で,表示された広告がクリックされたかどうかについて平均の差の検定を1000回行い.その時のp値の分布がどうなっているのかを計測します.平均値が等しい,のような単純な帰無仮説のもとではp値は一様分布に従います.しかしながら,結果を見てみると下の図のようになり,一様分布に従うとはいえなさそうです.
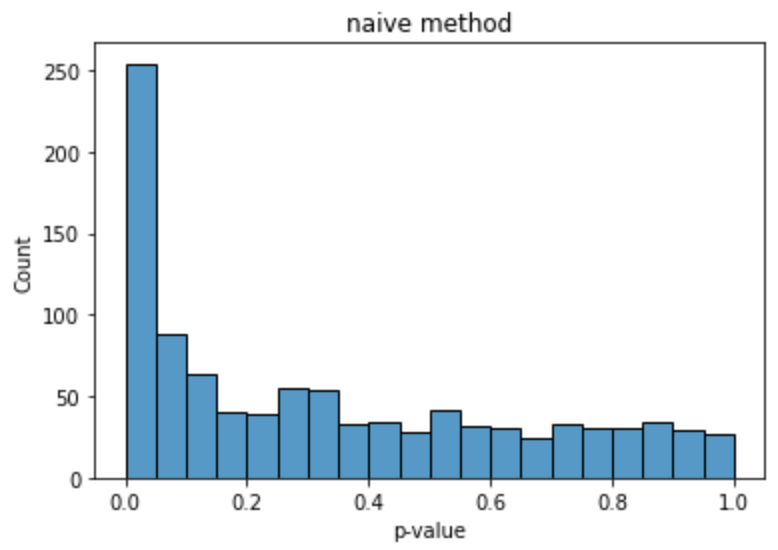
A/Aテストでは両者に差が存在しないにもかかわらず,明らかにp値が小さい値を取る回数が多くなっており,有意であると判定される回数が多くなっています.この検定結果を基に意思決定を下すのはちょっと怪しさがありますよね.
デルタ法を用いた場合
次に,こちらの論文の(6)式を用いて分散を推定し,その結果を用いて,平均の差の検定を行います.ポイントは,正規分布に従う2つの平均の比とみなし,その分散をデルタ法を用いて求めることにあります.同様に,p値の分布を計測した結果は下のとおりです.
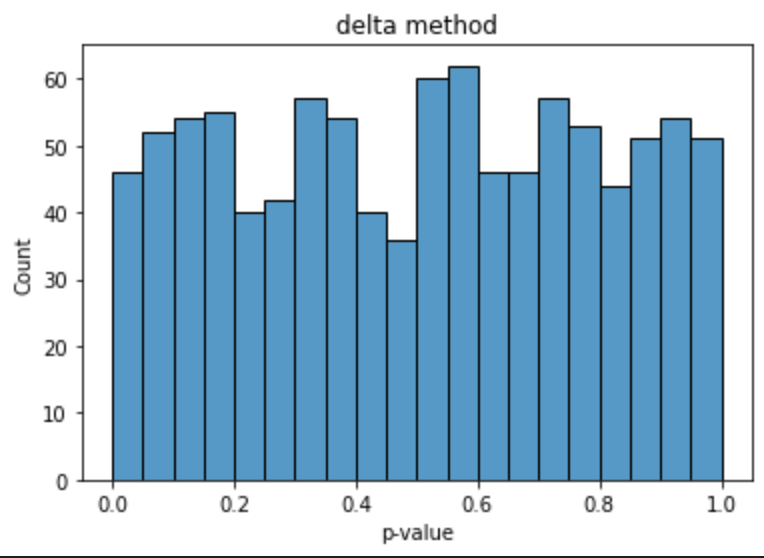
ナイーブなやり方で検定を行った場合に比べ,p値が小さい値を取る回数は減り,一様分布に近くなっていることが見て取れ,分散の過小評価が解消されていることが見て取れるかと思います.一様分布に近いかどうかを定量的に評価するため,追加で適合度検定を行ってみても良いかもしれません.
まとめ
今回は広告クリックのシミュレーションを行い,A/Bテストが失敗してしまうケースを紹介しました.A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実験とは では,A/Bテストについて網羅的に書いてあるので,A/Bテストを頻繁に行う方は一度目を通しておくと良いかなと思います.
今回のソースコード全体はこちらにおいてあるのでもし興味があれば見てみてください.また,誤りがあればぜひ教えていただけるとありがたいです!